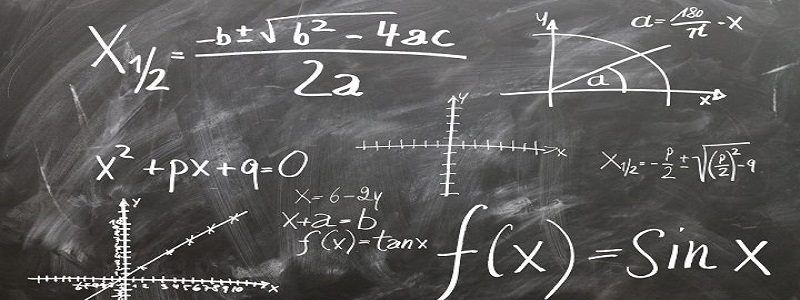Mathematics and Argument

Mathematics education has over the past 15 years increasingly elevated argumentation. The National Council of the Teachers of Mathematics established five ‘process standards’ for mathematical proficiency, and two of them (40%) are closely connected to argument: ‘reasoning and proof’ and ‘communications.’ As part of mathematical ‘reasoning and proof,’ students must be able to:

• • • ‘Develop and evaluate mathematical arguments and proofs’
    • ‘Select and use various types of reasoning and proofs’

As part of mathematical ‘communications,’ students must be able to:

• • • ‘Analyze and evaluate the mathematical thinking and strategies of others’
    • ‘Explanations should include mathematical arguments and rationales, not just procedural descriptions or summaries’

The Common Core Standards took mathematical argument – ‘a line of reasoning that intends to show or explain why a mathematical result is true,’ according to the Encyclopedia of Mathematics Education (Springer Media, 2014) – a step further when in their Standards of Math Practice 3 they require that students demonstrate a proficient ability to ‘construct viable arguments and critique the reasoning of others.’

Deductive vs. Inductive Arguments

The algebraic number sequences and series unit gives us an opportunity to investigate differences in the basic ‘types of reasoning’ recognized by authorities in argument education. One fundamental dichotomy in the field separates deductive arguments and inductive arguments.

by Dave Stuart Jr.

When I tell students and parents that we’ll be arguing a lot this year, I quickly need to stress that the kind of argument I’m talking about is beautiful. It is deep, critical, collaborative cognition. I pray all my students – and all humans, really — become adept at it because it makes us better people.

If any of that seems strong to you, it’s likely because you and I carry different definitions of “argument” in our heads. In Teaching the Argument in Writing, Richard Fulkerson puts it in a way that has stuck with me:

The goal [of argument] is not victory but a good decision, one in which all arguers are at risk of needing to alter their views, one in which a participant takes seriously and fairly the views different from his or her own.

In other words, argument allows us to:

• make better decisions and
• practice virtues like open-mindedness (“takes seriously”), fairness, and humility (“at risk of needing to alter their views”).

As part of a periodic series in The Debatifier on argument and math, today’s post backs up a step from Conor Cameron’s previous post on ‘Sometimes, Always, Never’ questioning in Algebra as a form of argument-making, and examines the broad and now well-established move in K-12 mathematics education toward thinking and reasoning skills at the base of mathematical formulas, procedures, and algorithms. The clear implication of this pedagogical direction is that students should be regularly engaging in argumentation in the classroom, as the articulation and performance of this thinking and reasoning.

Mathematics is constructed on a foundation of logical reasoning, and the National Council of the Teachers of Mathematics (NCTM) has been calling for an elevation of reasoning and argumentation in math education since at least 2000. Formal logic and the mathematical proof share an origin story, and the most influential figure in argument studies over the past 60 years, Stephen Toulmin (creator of the ‘Claim – Data/Evidence – Warrant/Reasoning’ argument model), had as his primary objective to expand the role and influence of informal logic.

By Conor Cameron

The Common Core State Standards demand that students of mathematics, “Construct viable arguments and critique the reasoning of others.” In a vacuum, that requirement probably seems more descriptive of what might occur in an English or social studies classroom. Many math teachers probably think to themselves, “Students may do that sort of work in their Geometry classes, not so much in mine.”

By Gerald Graff

“Hey, I’m all for teaching argument and debate,” my colleague assured me after viewing the ACE website. “But students have to know something about a topic before they can usefully debate it, and students these days just don’t.”

It’s one of the most familiar objections to organizing school and college curricula around debatable issues: until students know enough of the relevant information—as today’s students rarely do—they aren’t ready to debate such issues.     And it’s certainly true up to a point: it’s hard to enter a debate about whether income inequality is a problem or not if you lack information about what’s been happening to income distribution over the last generation.

What this way of thinking ignores, however, is its circularity: yes, students need some economic knowledge to intelligibly debate the pros and cons of income inequality, but unless they are exposed to the debate they may not see the point of acquiring that data in the first place.